Appoggiando la mano sulla roccia della caverna, spruzzando con la bocca acqua colorata di ocra, l’Homo Sapiens per la prima volta lasciava volontariamente l’impronta della mano, la testimonianza della sua esistenza. Decine di migliaia di anni sono passati, gli strumenti che si usano oggi sono solo in parte diversi, ma quella volontà di segnare su qualche cosa di eterno un segno che dimostrasse l’individualità soggettiva di una temporanea esistenza è rimasta come caratteristica propria dell’uomo.
Il segno prodotto del gesto ne è il risultato; descrive nel suo concretizzarsi l’ultima condizione non più legata al movimento ma dichiarazione di un’azione avvenuta. L’immagine ha da sempre rappresentato la duplice particolarità della natura umana: pensiero - azione, anima - corpo, mente - cervello, consapevolezza - istinto, conscio - inconscio. Nonostante le nuove tecnologie propongano una realtà codificata attraverso algoritmi, ogni segno non è altro che la dimostrazione di una espressione individuale.
Il segno, l’impronta è un evento, una sintesi oggettiva, un traccia di un’esistenza o di una volontà che attraverso di esso si esprime; è l’espressione di in un modello sintetico di una realtà temporale e fisica. L’impronta, il segno, l’orma, la caratteristica, lo spirito sono sinonimi di un fatto che si esprime in modo sintetico in cui sono riscontrabili le condizioni che l’hanno determinato e diventano modello di una realtà fisica o di una volontà espressiva.
Il modello, che sia matematico, economico, sociale, artistico, è un segno, un’impronta sintetica espressione della particolarità che diventa emblema di una qualità generalizzabile e condivisibile, da cui si può dedurre il concetto generale che rende l’analisi di un fatto tipologica. L’impronta del cervo è comune a tutti i cervi; attraverso la sua impronta il cacciatore deduce la tipicità propria della specie a cui associa le qualità prima generiche della razza e poi singolari dello specifico cervo.
Vitruvio nel De Architectura descrive come con l’uso della riga e del compasso sia possibile costruire l’ichnographia, l’immagine su di una pergamena dell’impronta lasciata dall’edificio sul terreno. Questa descrizione testimonia quanto sia stretto il rapporto tra disegno e segno, impronta conclusa di un processo mentale progettuale che trova nel modello rappresentato la sua prima realizzazione.
Le impronte del modello
L’impronta è sintesi del modello in alcune sue qualità; a differenza dell’impronta animale o dell’impronta umana, unica della forma che l’ha generata, le contemporanee “impronte digitali” possono essere molteplici. Attraverso esatti processi individualmente concepiti, è possibile risalire al modello, all’orma che ha generato l’impronta.
Prendiamo come caso studio gli skylines delle moderne città, sempre più ricchi di architetture che nelle forme sono assimilabili a grandi oggetti di design: architetture dall’andamento complesso caratterizzate da doppia curvatura ed assenza di spigoli per le quali la struttura in maniera indubbia segue la forma, che a sua volta avvolge espressivamente le funzioni.
Al di là di ogni giudizio critico sull’eticità di tali progetti e sul loro rapporto con il contesto, non si può negare come queste stimolino la produzione architettonica a continue innovazioni, in modo da poter realizzare anche i più arditi orgasmi architettonici.
I problemi che gravano sugli operatori che realizzano le forme sono inizialmente due: ideare un apparato strutturale in armonia con la complessità della forma e parallelamente, la pannellizzazione della stessa per descrivere la sinuosità delle forme.
A supporto del ragionamento portiamo all’attenzione tre modelli. Il primo lo chiameremo modello concettuale, modello genitore di altri due che su di esso saranno improntati; rispettivamente chiameremo gli altri modello strutturale e modello suddiviso.
Tema ricorrente per chi si occupa della messa in opera di queste architetture è l’operazione di Reverse Modeling per passare dal modello figlio ai modello genitore: quindi passare dall’impronta al fenomeno che l’ha generata.
Il workflow progettuale potrebbe essere sintetizzato nella seguente maniera. Una fase concettuale in cui la forma viene schizzata, disegnata, prototipata, rilevata proponendo un rapido passaggio da un modello all’altro per ottenere un modello digitale della forma concettuale in grado di assolvere le richieste della committenza e del progettista, problema ampiamente trattato in altri nostri scritti. La topologia del modello concettuale a nostro avviso deve racchiudere in se le geometrie dei modelli che verranno.

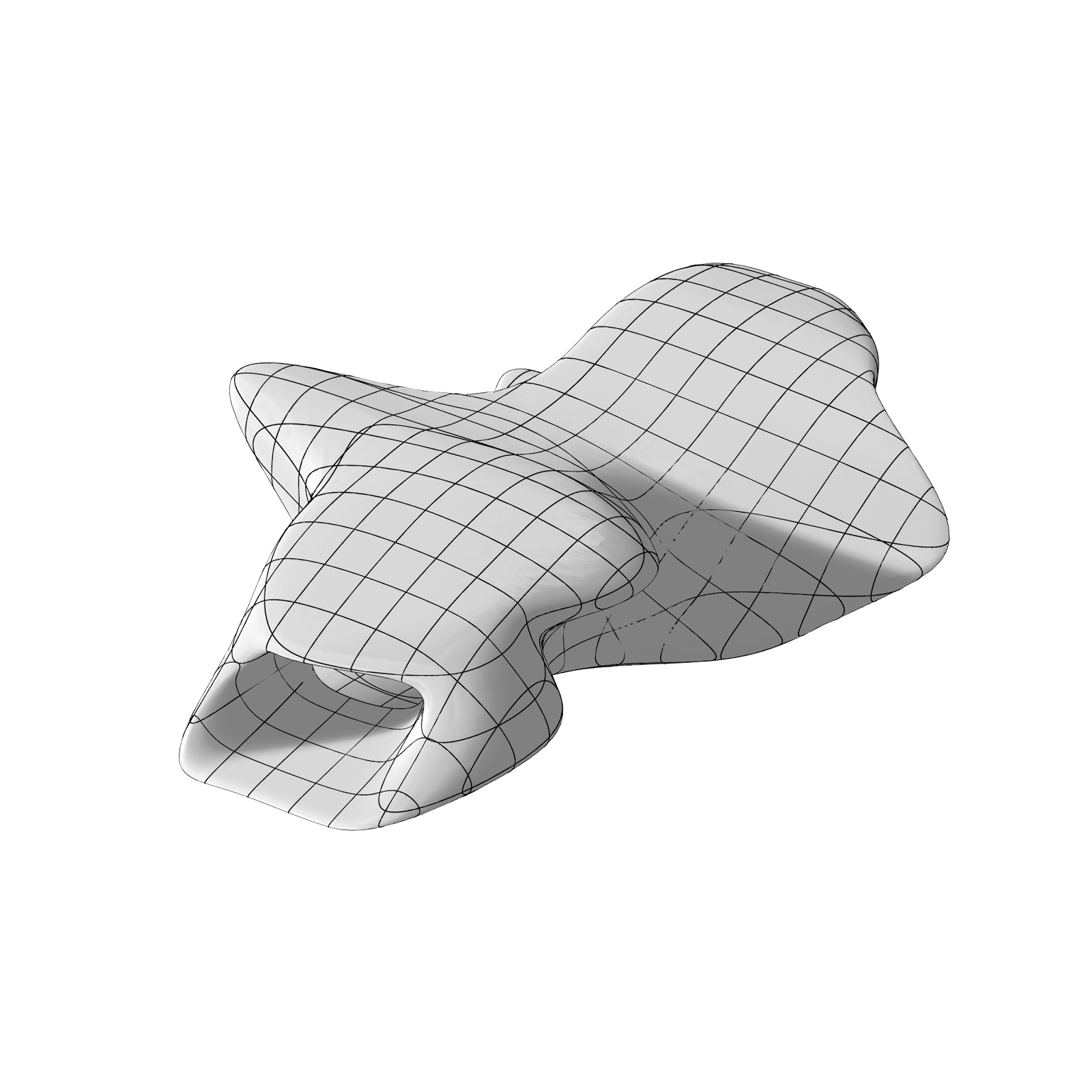
Il primo passo è creare il modello concettuale che, nel caso preso in esame sia in grado di inviluppare le funzioni. Il modello concettuale parte da una primitiva nurbs, l’ellissoide nel caso in figura 1. La scelta di questa primitiva è fondamentale per almeno due ragioni: da una parte essendo un solido ad unica superficie propone grande duttilità e trasformabilità, al contrario di qualunque polisuperficie che per sua natura genera spigoli ponendo limiti alla continuità; in secondo luogo identifichiamo sin da subito l’orientamento delle curve grafiche che “pettineranno” la forma.
Attraverso un processo di digital sculpting si passerà dalla primitiva alla forma voluta, il modello concettuale.
Questo metodo esecutivo consente di controllare alcuni ingredienti fondamentali dei modelli nurbs quali le isoparametriche, linee grafiche che segnano le superfici identificando l’orientamento del dominio lungo u e v della superficie. Al termine delle operazioni di morphing avremo una forma decisamente ordinata e maggiormente utile per chi si occupa di produzione dell’architettura.

Il modello concettuale diventa la forma sul quale improntare il modello suddiviso ed il modello strutturale, questi modelli saranno investiti da operazioni di facade engineering e structure engineering, discipline sempre più in auge per risolvere le nuove forme concettuali delle architetture unendo soluzioni tecnologiche innovative, alla comprensione delle geometrie complesse delle architetture. Nella maggior parte dei casi il modello di suddivisione ed il modello strutturale coincidono nelle prime scelte geometriche, differenziandosi a livelli successivi di approfondimento progettuale e tecnologico.
Il modello strutturale, in questa esperienza, parte dall’estrazione di curve caratteristiche della forma. Le curve diventeranno binari lungo i quali far scorrere profili scelti per creare polisuperfici che rappresenteranno la tramatura strutturale.
Le curve di profilo sono estratte dalla forma concettuale partendo da due logiche differenti: da una parte vi è la possibilità di affettare la forma perpendicolarmente ad una terna triortogonale, per la quale uno degli assi è disposto in direzione longitudinale al modello concettuale (fig. 2); dall’altra si rispetta il disegno delle isoparametriche che rappresentano la matematica della superficie (fig. 3). Il primo caso genera curve piane da utilizzate come direttrici delle sezioni di travi scelte, quindi facilmente producibili con frese e pantografi industriali ed una volta portate in opera, incontrano le travi appartenenti a fasci di piani ortogonali in intersezioni che si risolvono in modi spesso artigianali e non preventivabili. Inoltre la parcellizzazione risultante tra le maglie non è sempre quadrilatera.
L’algoritmo progettato per affettare il modello con piani paralleli ai piani ordinati XY, XZ e YZ è attuato e facilmente visualizzato attraverso l’utilizzo di sistemi nodali che alcuni software di rappresentazione digitale propongono. Per creare curve piane costruiamo innanzi tutto un parallelepipedo limite alla forma ideata. Di questo estrapoliamo tre spigoli convergenti verso lo stesso vertice, spigoli tutti ortogonali tra loro per costruzione. Ogni spigolo orienterà fasci di piani paralleli, costituendone la direzione normale; il numero dei piani è un valore dato dal progettista in relazione all’orditura strutturale desiderata e richiesta da opportuni calcoli.
Le sezioni che si otterranno sono curve piane per le quali si propone un offset esterno dello spessore pari al profilo scelto. Tra la curva sezione e la curva di offset si interporrà una superficie che opportunamente estrusa proporrà la struttura solida (fig. 4).
Una volta creato il modello strutturale è necessario creare il modello suddiviso coerente per la pannellizzazione delle parti che si inseriscono nelle maglie del modello strutturale. Il modello concettuale, che ricordiamo essere una superficie unica, è suddiviso utilizzando le curve piane precedentemente estrapolate, creando pannelli in grado di chiudere gli interstizi della maglia strutturale. Ogni singolo elemento frutto della suddivisione, è una superficie tagliata e come tale conserva l’intera matematica del modello concettuale, ne tiene memoria (fig. 5). I pannelli che si creano possono essere a tre a quattro o a più bordi, ed essendo porzione visibile del totale non visibile, è possibile fondere i pannelli non coerenti.

Passiamo adesso alla descrizione del modello strutturale derivante dall’individuazione, nel modello concettuale, di curve gobbe. Le curve gobbe prese in considerazione sono alcune isoparametriche della superficie (fig. 3). Le superfici matematiche nurbs sono entità che vivono in uno spazio parametrico R2, per cui ogni punto che si trova sulla superficie è individuabile attraverso l’interpolazione di due parametri: u e v. Se immaginiamo di mantenere fisso il parametro u e variamo il parametro v identifichiamo infiniti punti il cui luogo geometrico sulla superficie è la curva isoparametrica. Ad ogni parametro u scelto sul bordo della superficie considerata, corrisponderà una curva isoparametrica che connetterà bordi opposti. Stessa cosa accade per i parametri v scelti. Con questa procedura disegnamo un’orditura di curve che connettono bordi opposti proponendo spazi interstiziali sempre quadrilateri, orditura di cui è determinabile la partenza ma non il percorso nella superficie, fortemente condizionato dalla diversa densita dello spazio parametrico R2 della superficie, dovuta alle operazioni di morphing. Le considerazioni appena fatte se applicate sulla superficie complessa in figura, ci consentono di istruire algoritmi nodali in grado di creare la nuova struttura. Proviamo poi a darle corpo utilizzando sezioni circolari che seguono meglio le curve gobbe estratte dalla superficie (fig. 6).

Costruiamo il modello di suddivisione, il taglio lungo le isoparametriche propone pannelli che nel modello geometrico trattato identificano tasselli di superfici non tagliate, quindi non sarà possibile risalire alla forma che l’ha generata, dando però luogo a superfici decisamente leggere e manipolabili.
Il Reverse Modeling per risalire al modello dell’impronta
Ricordando che l’impronta è il segno lasciato da un corpo premuto su un materiale cedevole; la traccia di un modello su un altro. Notiamo che esiste un rapporto gerarchico tra i modelli in gioco: un modello A che segna ed un modello B che viene segnato. Nella nostra trattazione A è il modello concettuale e B è il modello strutturale (BI) o il modello suddiviso (BII).
Problema ricorrente nella produzione di architetture complesse è il passaggio dal modello strutturale al modello suddiviso. Un motivo tra tanti è quello di poter proporre un preventivo dei costi di un opera a partire dal disegno della struttura; i pannelli da montare tra le maglie della struttura hanno una grande incidenza sui costi, e per questo devono essere prefigurati nel numero e nella forma. Il passaggio dall’impronta BI all’impronta BII non può avvenire se non passando per il modello A generante.
Il modello strutturale a disposizione è quello in figura 7; notiamo che l’orditura è composta da travi che non hanno andamento curvilineo, ma si sviluppano lungo una spezzata, determinando per ogni segmento di trave una torsione minima. In questo modo l’orditura strutturale discretizza l’andamento gobbo delle isocurve memoria del modello concettuale. Si parte quindi dall’impronta strutturale dalla quale si vuole risalire al modello concettuale continuo. Il primo passo è la ricerca di un algoritmo per astrarre dalle travi i vertici delle spezzate direttrici; i punti trovati potranno essere interpolati con curve il cui andamento e forma restituiranno la superficie concettuale (fig. 8). Le curve differenziate in due fasci (il fascio u ed il fascio v), assieme alle curve di bordo individuate con un algoritmo simile, costituiscono la maglia sulla quale stendere una superficie tagliata con lo strumento patch. Questa è una delle possibili forme con cui può essere rappresentato il modello concettuale, la forma che ha generato l’impronta, la forma espressiva voluta dal progettista. Attraverso una semplice operazione di reverse modeling siamo risaliti dalla struttura alla forma, quindi dal modello BI al modella A.

Passiamo ora dal modello concettuale al modello suddiviso. La superficie pach per sua natura non inviluppa perfettamente le curve estratte dalla struttura, per questo motivo le curve vengono proiettate normalmente alla superficie in modo da farle aderire alla forma. Solo adesso le curve appartengono alla superficie e possono tagliarla generando una serie di pannelli, frammenti della forma generale, a doppia curvatura. Questioni di carattere tecniche, economiche e pratiche impongono la discretizzazione dei pannelli a doppia curvatura in porzioni piane capaci di raccontare la forma concettuale, ricostruendola in una superficie poliedrica leggermente distanziata dalla struttura per evitare collisioni. Estraiamo i bordi di ogni pannello e uniamoli ad identificare policurve chiuse con i vertici in evidenza. Spostiamo i vertici individuati lungo la direzione normale alla superficie nel punto in cui il vertice si trova; il valore dello spostamento è il distaccamento voluto dalla struttura, il verso sarà esterno all’orditura. I vertici spostati, essendo ordinati pannello per pannello possono creare le facce del poliedro in grado di assolvere i presupposti elencati in precedenza (fig. 9).

di Michele Calvano, Andrea Casale, Graziano Mario Valenti